RefinedTriLinear3DFiniteElement Class Reference

Class for refined trilinear FE on a hexahedron. More...

#include <fe.hpp>

Inheritance diagram for RefinedTriLinear3DFiniteElement:

Collaboration diagram for RefinedTriLinear3DFiniteElement:

List of all members.

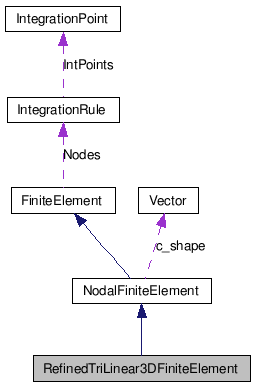
Public Member Functions
	RefinedTriLinear3DFiniteElement ()
	Construct a biquadratic FE on quadrilateral.
virtual void	CalcShape (const IntegrationPoint &ip, Vector &shape) const
virtual void	CalcDShape (const IntegrationPoint &ip, DenseMatrix &dshape) const

---

Detailed Description

Class for refined trilinear FE on a hexahedron.

Definition at line 997 of file fe.hpp.

---

Constructor & Destructor Documentation

RefinedTriLinear3DFiniteElement::RefinedTriLinear3DFiniteElement

(

)

Construct a biquadratic FE on quadrilateral.

Definition at line 4084 of file fe.cpp.

References IntegrationRule::IntPoint(), FiniteElement::Nodes, IntegrationPoint::x, IntegrationPoint::y, and IntegrationPoint::z.

---

Member Function Documentation

void RefinedTriLinear3DFiniteElement::CalcDShape	(	const IntegrationPoint &	ip,
		DenseMatrix &	dshape
	)		const [virtual]

virtual function which evaluates the values of all partial derivatives of all shape functions at a given point ip and stores them in the matrix dshape (Dof x Dim) (9 x 2) so that each row contains the derivatives of one shape function

Implements FiniteElement.

Definition at line 4262 of file fe.cpp.

References IntegrationPoint::x, IntegrationPoint::y, and IntegrationPoint::z.

void RefinedTriLinear3DFiniteElement::CalcShape	(	const IntegrationPoint &	ip,
		Vector &	shape
	)		const [virtual]

virtual function which evaluates the values of all shape functions at a given point ip and stores them in the vector shape of dimension Dof (9)

Implements FiniteElement.

Definition at line 4129 of file fe.cpp.

References IntegrationPoint::x, IntegrationPoint::y, and IntegrationPoint::z.

---

The documentation for this class was generated from the following files:

• fe.hpp
• fe.cpp