RT0HexFiniteElement Class Reference

#include <fe.hpp>

Inheritance diagram for RT0HexFiniteElement:

Collaboration diagram for RT0HexFiniteElement:

List of all members.

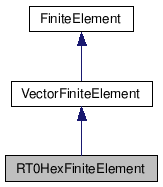
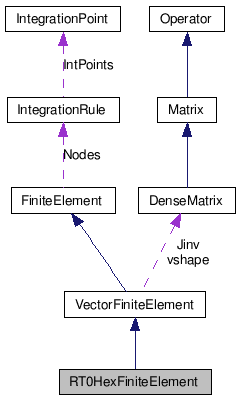
Public Member Functions
	RT0HexFiniteElement ()
virtual void	CalcVShape (const IntegrationPoint &ip, DenseMatrix &shape) const
virtual void	CalcVShape (ElementTransformation &Trans, DenseMatrix &shape) const
virtual void	CalcDivShape (const IntegrationPoint &ip, Vector &divshape) const
virtual void	GetLocalInterpolation (ElementTransformation &Trans, DenseMatrix &I) const
virtual void	Project (VectorCoefficient &vc, ElementTransformation &Trans, Vector &dofs) const
Static Private Attributes
static const double	nk [6][3]

---

Detailed Description

Definition at line 1061 of file fe.hpp.

---

Constructor & Destructor Documentation

RT0HexFiniteElement::RT0HexFiniteElement

(

)

Definition at line 4824 of file fe.cpp.

References IntegrationRule::IntPoint(), FiniteElement::Nodes, IntegrationPoint::x, IntegrationPoint::y, and IntegrationPoint::z.

---

Member Function Documentation

void RT0HexFiniteElement::CalcDivShape	(	const IntegrationPoint &	ip,
		Vector &	divshape
	)		const [virtual]

This virtual function evaluates the divergence of all shape functions at the given IntegrationPoint. The result is stored in the Vector divshape (of size Dof).

Reimplemented from FiniteElement.

Definition at line 4884 of file fe.cpp.

virtual void RT0HexFiniteElement::CalcVShape	(	ElementTransformation &	Trans,
		DenseMatrix &	shape
	)		const [inline, virtual]

Reimplemented from FiniteElement.

Definition at line 1072 of file fe.hpp.

References VectorFiniteElement::CalcVShape_RT().

void RT0HexFiniteElement::CalcVShape	(	const IntegrationPoint &	ip,
		DenseMatrix &	shape
	)		const [virtual]

This virtual function evaluates the values of all components of all shape functions at the given IntegrationPoint. The result is stored in the DenseMatrix shape (Dof x Dim) so that each row contains the components of one shape function.

Reimplemented from FiniteElement.

Definition at line 4854 of file fe.cpp.

References IntegrationPoint::x, IntegrationPoint::y, and IntegrationPoint::z.

Referenced by GetLocalInterpolation().

void RT0HexFiniteElement::GetLocalInterpolation	(	ElementTransformation &	Trans,
		DenseMatrix &	I
	)		const [virtual]

Return the local interpolation matrix I (Dof x Dof) where the fine element is the image of the base geometry under the given transformation.

Reimplemented from FiniteElement.

Definition at line 4898 of file fe.cpp.

References CalcAdjugateTranspose(), CalcVShape(), FiniteElement::Dim, FiniteElement::Dof, IntegrationRule::IntPoint(), ElementTransformation::Jacobian(), VectorFiniteElement::Jinv, mfem_error(), nk, FiniteElement::Nodes, ElementTransformation::SetIntPoint(), ElementTransformation::Transform(), VectorFiniteElement::vshape, IntegrationPoint::x, IntegrationPoint::y, and IntegrationPoint::z.

void RT0HexFiniteElement::Project	(	VectorCoefficient &	vc,
		ElementTransformation &	Trans,
		Vector &	dofs
	)		const [virtual]

Given a vector coefficient and a transformation, compute its projection (approximation) in the local finite dimensional space in terms of the degrees of freedom. (VectorFiniteElements)

Reimplemented from FiniteElement.

Definition at line 4951 of file fe.cpp.

References CalcAdjugateTranspose(), FiniteElement::Dim, VectorCoefficient::Eval(), IntegrationRule::IntPoint(), ElementTransformation::Jacobian(), VectorFiniteElement::Jinv, nk, FiniteElement::Nodes, and ElementTransformation::SetIntPoint().

---

Member Data Documentation

const double RT0HexFiniteElement::nk [static, private]

Initial value:

{{0,0,-1}, {0,-1,0}, {1,0,0}, {0,1,0}, {-1,0,0}, {0,0,1}}

Definition at line 1064 of file fe.hpp.

Referenced by GetLocalInterpolation(), and Project().

---

The documentation for this class was generated from the following files:

• fe.hpp
• fe.cpp